정밀도와 민감도
- 분류기를 설계하다 보면 분류기의 성능을 평가할 필요가 있습니다. 보통 분류 작업에 대해 이를 수행할 분류기를 하나만 만들지 않기 때문입니다. 또는 다른 사람에게 본인이 만든 분류기가 어느 정도의 성능을 갖고 있는지 설명할 필요가 있습니다.
정확도의 함정
- 정확도는 정답을 맞춘 비율을 의미합니다. 즉
A를A라고 대답한 비율을 의미하죠. 하지만 여기에는 큰 함정이 있습니다. 다음과 같은 상황을 살펴볼까요? 10,000개의 샘플이 있고, 불량 샘플을 찾는 문제라고 가정해보겠습니다.10,000개의 샘플 중 불량 샘플은500개가 있습니다. 가장 빠르고 정확도만을 기준으로 삼는 분류기는 무엇이 있을까요? 바로 모든 샘플을 정상 샘플로 분류하는 분류기일겁니다. 사실 이러한 분류기는 분류기라 부르기도 힘듭니다. 분류라는 판단 근거나 로직 없이 신호가 들어오면 무조건 정상이라 응답하니깐요.- 놀랍게도 이 분류기의 정확도는
95%입니다. 왜 그럴까요?10,000개의 샘플 중 불량 샘플500개를 정상으로 분류했고, 정상인 샘플은 모두 정상 샘플로 올바르게 분류했기 때문입니다. 즉 불량 샘플을 하나도 찾지 못했지만 정상 샘플을 정상 샘플이라고 응답한 결과가 많아, 정확도는 높게 나오는 아이러니한 상황이 발생합니다.
정밀도와 재현율
- 위와 같은 이유로 분류기를 평가할 때 정확도는 잘 사용하지 않습니다. 특히 데이터의 비율이 서로 다르다면 큰 문제가 발생합니다. 이럴 때 분류기의 성능을 확인하는 지표로 정밀도(Precision)와 재현율(Recall)을 많이 사용합니다. 그러면 정밀도와 재현율은 무엇일까요?
오차 행렬(Confusion Matrix)
- 정밀도와 재현율을 이해하기 위해서는 오차 행렬(Confusion Matrix)이 무엇인지 알고 있어야 합니다. 또 오차 행렬을 알고 있으면 정밀도와 재현율을 쉽게 이해할 수 있습니다. 아래 그림과 같은 행렬을 오차 행렬이라 합니다.
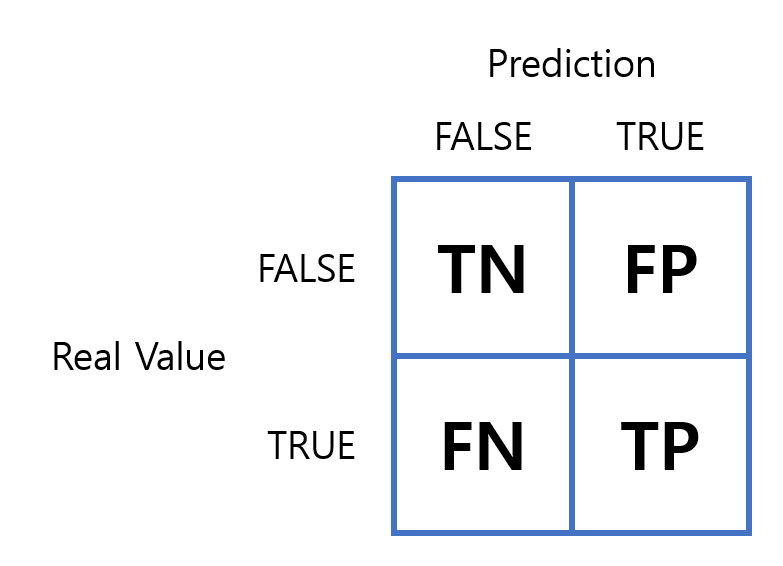
오차 행렬의 행은
Real Value로 실제 값을 의미합니다.오차 행렬의 열은
Prediction으로 분류기의 예측 값을 의미합니다.오차 행렬의 요소는
TN,FP,FN,TP로 각각의 의미는 다음과 같습니다.- TN(True Negative): 분류기는 False로 분류했고, 실제로도 False인 경우
- 위와 같은 문제에서 분류기는 정상 샘플이라 분류했고, 실제로도 정상 샘플인 경우를 의미합니다. 여기서 False나 True는 분류기의 설계에 따라 다릅니다. 여기서는 분류기가 불량 샘플을 True라고 예측할 것이라고 정의하였습니다.
- FP(False Positive): 분류기는 True로 분류했지만, 실제로는 False인 경우
- 분류기가 불량 샘플이라 분류했지만, 실제로는 정상 샘플인 경우
- FN(False Negative): 분류기는 False로 분류했지만, 실제로는 True인 경우
- 분류기가 정상 샘플이라 분류했지만, 실제로는 불량 샘플인 경우
- TP(True Positive): 분류기는 True로 분류했고, 실제로도 True인 경우
- 분류기가 불량 샘플이라 분류했고, 실제로도 불량 샘플인 경우
- TN(True Negative): 분류기는 False로 분류했고, 실제로도 False인 경우
앞서 설명한 문제와 같이 모든 샘플을 False로 분류하는 분류기의 오차 행렬은 다음과 같은 결과가 나올겁니다.
- TN:
9,500 - FP:
0 - FN:
500 - TP:
0
- TN:
오차 행렬에서 정확도의 수식은 $$Accuracy = \frac{(TN + TP)}{(TN + FP + FN + TP)}$$ 이므로
95%의 정확도를 나타냅니다. 반대로 정밀도와 재현율은 어떨까요?
정밀도(Precision)
- 정밀도는 분류기가 True로 예측한 샘플들 중, 실제 샘플이 True인 비율입니다. 수식으로는 다음과 같이 작성합니다.
$$ Precision = \frac{TP}{TP + FP} $$
- 앞서 작성한 오차 행렬에서 TP와 FP의 값이 모두
0이므로 분류기의 정밀도는0입니다. 정확도는95%이지만 정밀도는0%인 형편없는 분류기였던 것이였죠.
재현율(Recall)
- 재현율은 실제 True인 샘플들 중에서 분류기가 True라고 예측한 비율입니다. 수식으로는 다음과 같이 작성합니다.
$$ Recall = \frac{TP}{TP + FN} $$
- 앞서 작성한 오차 행렬에서 TP는
0, FN은500이므로 재현율도0%입니다.
\(F_{1}\) 점수
- \(F_{1}\) 점수(\(F_{1}\) Score)는 정밀도와 재현율을 하나의 값으로 보기 위한 값입니다. 정밀도와 재현율의 조화 평균(Harmonic Mean)을 계산하면 이 값이 \(F_{1}\) 점수입니다. 수식으로는 다음과 같습니다.
$$ F_{1} = \frac{2}{\frac{1}{Precision} + \frac{1}{Recall}} = \frac{TP}{TP + \frac{FN + FP}{2}} $$
- \(F_{1}\) 점수는 정밀도와 재현율의 비율이 비슷하면 높은 값을 갖는 특징이 있습니다. 하지만 \(F_{1}\) 점수가 무조건 좋다고 좋은 분류기는 아닙니다. 문제에 따라 정밀도와 재현율을 조절할 필요가 있습니다. 정밀도와 재현율의 트레이드오프가 이와 같은 경우입니다.
정밀도와 재현율 트레이드 오프
- 분류기는 항상 정밀도와 재현율의 트레이드 오프(Trade-Off)를 갖고 있습니다. 분류기는 입력된 값을 기준으로 계산하고 일종의 **결정 함수(Decision Function)**을 사용하여 True/False 응답을 출력합니다. 즉 일정 기준을 만족하면 해당 응답에 대해 True를 반환하고, 아닌 경우에는 False를 반환합니다.
- 결정 함수에서 사용하는 기준으로 임계값(Threshold)이라는 표현을 많이 사용합니다.
- 즉 사용자는 분류기의 임계값을 조절하여 분류기의 출력을 조절할 수 있습니다. 여기서 분류기의 계산 결과를 신뢰 점수라고 표현하고, 신뢰 점수를 임계값과 비교하여 신뢰 점수가 임계값보다 높은 경우에 True를 반환하고, 반대의 경우에는 False를 반환합니다.
임계값을 낮출 경우
- 사용자가 임계값을 낮은 기준으로 조절하면 분류기는 True라고 응답하는 경우가 많아집니다. 즉
TP와FP가 높아지는 현상이 발생합니다. (True라고 응답한 결과들 중에서 실제 True인 경우가 있으므로 둘 다 상승합니다.) - 이 경우
FN은 줄어드니 (상대적으로FP와TP가 많아지므로) 재현율이 올라가는 현상이 발생합니다. (재현율의 수식을 다시 확인해보세요.)
$$ Recall = \frac{TP}{TP + FN} $$
임계값을 높일 경우
- 반대로 사용자가 임계값을 높은 기준으로 조절하면 분류기는 False라고 응답하는 경우가 많아집니다. 즉
TN과FN이 높아집니다. - 또한 분류기는 높은 신뢰 점수를 갖는 입력에만 True라고 응답하니
FP는 줄어들고TP가 높아집니다.
$$ Precision = \frac{TP}{TP + FP} $$
어떤 임계값을 설정해야 할까?
- 이처럼 임계값에 따라 정밀도와 재현율은 서로 반비례하는 관계를 갖습니다. 이러한 관계를 트레이드오프라고 표현합니다.
- 그렇다면 어떤 임계값이 좋을까요? 이는 문제에 따라 다릅니다.
- 방범 시스템의 경우 임계값을 낮춰 방범 시스템이 자주 작동하더라도, 도둑을 확실하게 잡는 것이 좋을겁니다. (높은 재현율, 낮은 정밀도)
- 반대로 인터넷 광고 차단 시스템인 경우에는 사용자가 유용한 광고를 몇 개 못보더라도, 불쾌한 불법 광고는 확실하게 차단하는 것이 좋은 경우일수도 있습니다. (낮은 재현율, 높은 정밀도)
- 높은 재현율과 높은 정밀도를 요구하는 시스템도 있습니다. 환자의 심각한 질병을 검사하는 검사기가 이러한 경우일겁니다. (물론 높은 정밀도와 높은 재현율을 갖는 시스템은 만들기가 무척 어렵습니다.)